1. Original image and convert to binary image
S = imread('img1.bmp');
S = im2bw(S);
imshow(S);
2. Perform Hough Transform and show the result
[H, theta,rho]=hough(S);
figure;
imshow(H,[],'xdata',theta,'ydata',rho);
xlabel('\theta'),ylabel('\rho')
axis on, axis normal;
title('Hough Matrix');
3. Count the "frequency" of the intensity of the Hough Matrix.
clear data;
for cnt = 1:max(max(H))
data(cnt) = sum(sum(H == cnt));
end
figure;
plot(data,'.');
The codes are applied to different images to compare the differences of
the Hough Matrix on different objects' shapes.
Some simple objects' shape and their Hough Matrix are as follow:
a. Single Point
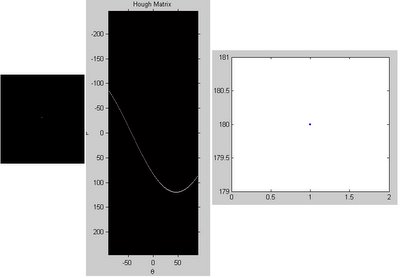
To obtain the Hough Transform, draw lines from -90 to 90 degree that cross the dot, follow by drawing a Perpendicular line from the upper left of the image to the line, and measure the lenght(rho) and the angle (theta) of the Perpendicular line.
The "hough" function will perform this for every 1 degree, and hence, for a single dot, the there will be 180 of '1' in the "Hough Matrix".
b. Two Points 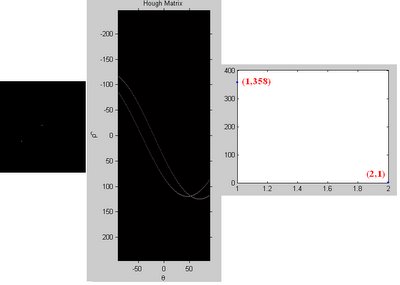
When there are two points on an image, the Hough Matrix consist of 2 lines, and interect at a point which is a line that link the 2 points together in x-y plane (left figure).
Since there is only one intersection (only one line that link 2 points together), the frequencies of '1' in Hough Matrix is 358, while the frequencies of '2' is 1 in the Hough Matrix. (the '1' and '2' indicates how many time a rho-theta appear in the Hough Matrix)
c. Line
A line consists of numbers of points, ideally (the line is 45 degree) the intersection in the Hough Matrix will have the intensity same as the line lenght.
Hough Transform always used to detect lines in a real image, in which the edges always distorted. A higher value in the Hough Matrix indicates the higher possibility of the existence of a straight line.
More objects shapes will be shown in the next post...