Simple Code for Hough Transform

Previous few examples using the Hough Transform function to perform the operation. However, Hough Transform function only available in new version of the tools. For those who are still using older version, this example shows a simple way of performing Hough Transform with a few lines of codes.

1. Reading image and the convert to binary image. After that, the location of the value '1' is found using 'find' function. (assume the image is already preprocess, if not, the 'edge' function might help)

I = imread('pic20.jpg');
I =im2bw(I);
[y,x]=find(I);
[sy,sx]=size(I);
imshow(I);



2. Find all the require information for the transformatin. the 'totalpix' is the numbers of '1' in the image, while the 'maxrho' is used to find the size of the Hough Matrix

totalpix = length(x);
maxrho = round(sqrt(sx^2 + sy^2));

3. Preallocate memory for the Hough Matrix. The resolution for both rho and theta are set to one.

HM = zeros(2*maxrho,180);

4. Performing Hough Transform. Notice the accumulator is located in the inner for loop.

for cnt = 1:totalpix
cnt2 = 1;
for theta = -pi/2:pi/180:pi/2-pi/180
rho = round(x(cnt).*cos(theta) + y(cnt).*sin(theta));
HM(rho+maxrho,cnt2) = HM(rho+maxrho,cnt2) + 1;
cnt2 = cnt2 + 1;
end
end

theta = rad2deg(-pi/2:pi/180:pi/2-pi/180);
rho = -maxrho:maxrho-1;
imshow(uint8(HM),[],'xdata',theta,'ydata',rho);
xlabel('\theta'),ylabel('\rho')
axis on, axis normal;
title('Hough Matrix');


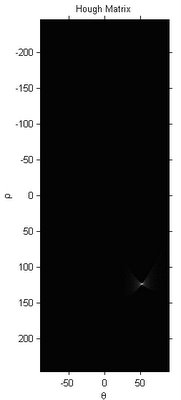
5. Done! However, the code is quite slow, anyway, it works!