The second approach would be more flexible especially when we want to modified the Hought Transform to detect other shape other than line. In this example, a modified version of Hough Transform is used to detect the circle instead of line.
In this case, instead of transforming the pixel to rho and theta domain, we use the circle equation --> (x-a)^2 + (y-b)^2 = R^2 to map the pixel to a-b domain. Let's see how to perform this:
1. Reading image and the convert to binary image. After that, the location of the value '1' is found using 'find' function. (assume the image is already preprocess, if not, the 'edge' function might help)
clear all;clc;
I = imread('pic20.bmp');
I =im2bw(I);
[y,x]=find(I);
[sy,sx]=size(I);
imshow(I);

2. Find all the require information for the transformatin. the 'totalpix' is the numbers of '1' in the image.
totalpix = length(x);
3. Preallocate memory for the Hough Matrix. Try to play around with the R, or the radius to see the different results.
HM = zeros(sy,sx);
R = 34;
R2 = R^2;
4. Performing Hough Transform. Notice the accumulator is located in the inner for loop. This portion of codes will map the original image to the a-b domain.
b = 1:sy;
for cnt = 1:totalpix
a = (round(x(cnt) - sqrt(R2 - (y(cnt) - [1:sy]).^2)));
for cnt2 =1:sy
if isreal(a(cnt2)) & a(cnt2)>0
HM(cnt2,a(cnt2)) = HM(cnt2,a(cnt2)) + 1;
end
end
end
5. Showing the Hough Matrix
imshow(HM,[]);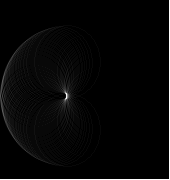
6. Finding the location of the circle with radius of R
[maxval, maxind] = max(max(HM));
[B,A] = find(HM==maxval);
imshow(I); hold on;
plot(mean(A),mean(B),'xr')