Hough Transform For Circle Detection - with unknown radius (II)

The detection of circle with unknown radius has been shown in previous post - Hough Transform For Circle Detection - with unknown radius (I) , by using a lot of "for" loops.

This example shows the same function with "vectorized" code, which run 25% faster than the previous code, in a Pentium M 1.5 GHz computer with 512 M RAM.

Let's see how to perform this:

1. Reading image and the convert to binary image. After that, the location of the value '1' is found using 'find' function. (Assume the image is already preprocess, if not, the 'edge' function might help)

clear all;clc;
I = imread('pic26.bmp');
I =im2bw(I);
[y,x]=find(I);
[sy,sx]=size(I);
imshow(I);



2. Find all the require information for the transformation. The 'totalpix' is the numbers of '1' in the image.

totalpix = length(x);

3. Pre-allocate memory for the Hough Matrix and other variables. The ‘R’ is known in the range from 1 to 50, so we reserve 50 "layers" for the HM matrix.

HM = zeros(sy*sx*50,1);
R = 1:50;
R2(1,1,:) = R.^2;
R2 = repmat(R2,[sy,totalpix,1]);
y = repmat(y',[sy,1,50]);
x = repmat(x',[sy,1,50]);
b = 1:sy;
b = repmat(b',[1,totalpix,50]);
a = zeros(sy,totalpix);

4. Performing Hough Transform. Do notice that no "for" loops are used here.

a. Find the a parameter

a = (round(x - sqrt(R2 - (y - b).^2)));

b. Find the location of ‘a’ and ‘b’, as well as the valid value both.

[xx,yy,zz]=find((imag(a)==0 & a>0));
b = b(imag(a)==0 & a>0);
a = a(imag(a)==0 & a>0);

c. Find the indices and remap it to different layers

ind = sub2ind([sy,sx],b,a);
ind = ind + (ceil(yy/totalpix)-1)*sx*sy;

d. Construct the Hough Matrix of 50 layers

val = ones(length(ind),1);
data=accumarray(ind,val);
HM(1:length(data)) = data;
HM2 = reshape(HM,[sy,sx,50]);

5. Find for the maximum value for each layer, or in other words, the layer with maximum value will indicate the corresponding ‘R’ for the circle.

for cnt = 1:50
H(cnt) = max(max(HM2(:,:,cnt)));
end
plot(H,'*-');



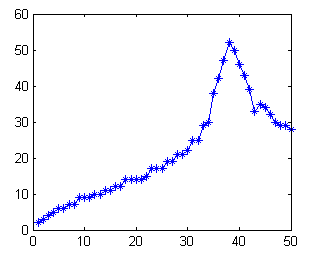
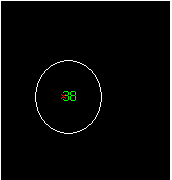
6. Extract the information from the layer with maximum value, and overlap with the original image.

[maxval, maxind] = max(H);
[B,A] = find(HM2(:,:,maxind)==maxval);
imshow(I); hold on;
plot(mean(A),mean(B),'xr')
text(mean(A),mean(B),num2str(maxind),'color','green')


7. This example use the vectorized code, and the speed of the program is 25 % faster than the previous example using "for" loops.