Hough Transform For Hyperbola Detection - with known eccentricity

More Hough Transform examples!

In last few examples, the Hough Transform are used to detect different shape, such as line and circle. For the circle detection, examples of circles with known radius detection and circles with unknown radius detection have been illustrated.

Besides, different techniques of implemeting the code are shown, as in "for" loops and vectorized code.

In this example, example of how the Hough Transform could be used for hyperbola detection would be demonstrated.

Firstly, let's see the equation of the hyperbola:

(x-xo)^2/a^2 - (y-yo)^2/b^2 = 1

Let's start with a simple example to find the asymptotes and the crossing point of a hyperbola with known eccentricity, e^2 = a^2 + b^2, and to simplified the problem, let's make the a = b = 29.

1. Reading image and the convert to binary image. After that, the location of the value '1' is found using 'find' function. (the image is in white background and black object, so the '~' is used to get the negative image.

clear all;clc;
I = imread('pic27.bmp');
I =im2bw(I);
imshow(I);
I = ~I;
[y,x]=find(I);
[sy,sx]=size(I);
imshow(I);

2. Find all the require information for the transformatin. the 'totalpix' is the numbers of '1' in the image

totalpix = length(x);

3. Preallocate memory for the Hough Matrix. In this case, the a and b are known as 29 (in pixels).

HM = zeros(sy,sx);
a = 29;
b = 29;

4. Performing Hough Transform to transform the x-y domain to xo-yo domain.

yo = 1:sy;

for cnt = 1:totalpix


% a. Four lines of equation here to detect the hyperbola shapes in 4
% different direction
xo(:,1) = round(x(cnt) + sqrt(a.^2.*(((y(cnt)-yo).^2/(b.^2))+1)));
xo(:,2) = round(x(cnt) - sqrt(a.^2.*(((y(cnt)-yo).^2/(b.^2))+1)));
xo(:,3) = round(x(cnt) + sqrt(a.^2.*(((y(cnt)-yo).^2/(b.^2))-1)));
xo(:,4) = round(x(cnt) - sqrt(a.^2.*(((y(cnt)-yo).^2/(b.^2))-1)));


% b. Since there are 4 equations, Hough Matrix must consists of the
% combination for 4 equation.
for cnt3 = 1:4
for cnt2 = 1:sy

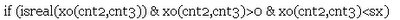
HM(cnt2,xo(cnt2,cnt3)) = HM(cnt2,xo(cnt2,cnt3)) + 1;

end
end
end

end

5. Showing the Hough Matrix

imshow(HM,[]);

6. Finding the asymptotes and the crossing point of a hyperbola

[maxval, maxind] = max(max(HM));
[Yo,Xo] = find(HM==maxval);
imshow(I); hold on;
plot(mean(Xo),mean(Yo),'xr')
c1 = mean(Yo) - mean(Xo);hold on;
plot(1:100, [1:100] + c1);
c2 = mean(Yo) + mean(Xo); hold on;
plot(1:100, -[1:100] + c2);

Y = 1:sy;
X = -sqrt(((Y-mean(Yo)).^2/a.^2 + 1).*b.^2) + mean(Xo);
hold on;
plot(X,real(Y),'r');