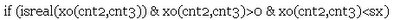Further more, life become more and more busy, and sometimes I really out of idea what to post here. :P
Until I receive some e-mail from some reader...
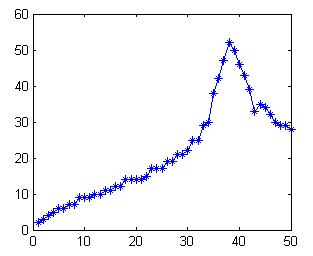
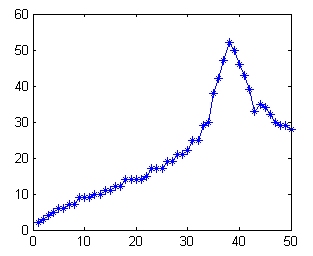
This is rather a simple example to measure a length of an object in an image. We could easily get the reading in pixels, and with a reference, we could just use a simple mathematic to compute the lenght in some standard unit.
Let's see this simple example:
1. Reading image and show the true color image.
clear all;clc;
I = imread('pic29.tif');
imshow (I);
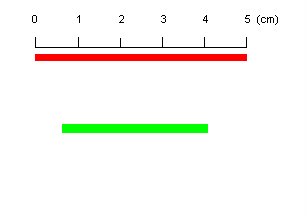
2. Assuming that we know the length of the red object (as reference) which is 5 cm, locate the red object with simple command and find the length in pixels:
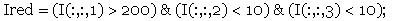 Ired_labeled = bwlabel(Ired);
Ired_labeled = bwlabel(Ired);Ired_props = regionprops(Ired_labeled);
Ired_length_in_pixel = Ired_props.BoundingBox(3);
disp(Ired_length_in_pixel);
212
3. To measure the length of the green object, extract the object:
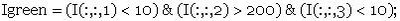 Igreen_labeled = bwlabel(Igreen);
Igreen_labeled = bwlabel(Igreen);Igreen_props = regionprops(Igreen_labeled);
Igreen_length_in_pixel = Igreen_props.BoundingBox(3);
disp(Igreen_length_in_pixel);
146
4. Calculate the length of green object in cm
Igreen_length_in_cm = Igreen_length_in_pixel/Ired_length_in_pixel*5;
disp(Igreen_length_in_cm);
3.4434

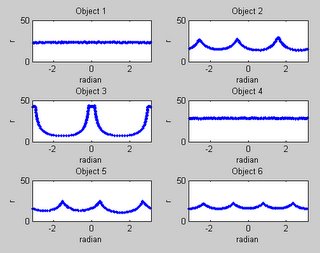
 Finally, the 5 by 7 matrices is concatenated into a stream so that it can be feed into network 35 input neurons. The input of the network is actually the negative image of the figure, where the input range is 0 to 1, with 0 equal to black and 1 indicate white, while the value in between show the intensity of the relevant pixel.
Finally, the 5 by 7 matrices is concatenated into a stream so that it can be feed into network 35 input neurons. The input of the network is actually the negative image of the figure, where the input range is 0 to 1, with 0 equal to black and 1 indicate white, while the value in between show the intensity of the relevant pixel.